Varyans



 Bu bölümde neler bulabilirsin?
1. Bölüm: Varyansın tanımı
2. Bölüm: Varyans hesaplamak neden önemlidir?
3. Bölüm: Örnek
4. Bölüm: SPSS uygulaması
5. Bölüm: Sonuçların yorumlanması
6. Bölüm: Sonuçların raporlaması
7. Bölüm: Kaynakça
İstatistiksel analizlerin çoğunda aritmetik ortalama merkezi eğilim ölçüsü olarak tercih edilir. Ancak ortalama tek başına yeterli bilgi içermez. Veri setindeki değerlerin bazıları aritmetik ortalamaya yakındır bazıları uzaktır. Böyle bir veride değerlerin aritmetik ortalama arasındaki farka sapma adı verilir (Alpar, 2016, s. 97). Ancak dağılımdaki tüm değerlerin aritmetik ortalamadan farkları hesaplandığında toplamlarının sıfıra eşit olduğu gözlemlenir. Bu sebeple, sapmaların kareleri alınarak problem çözüme kavuşur. Daha açık bir ifade ile bir veri setindeki değerlerin ortalamadan farklarının karelerinin ortalaması varyans olarak bilinir (Turgut ve Baykul, 2014, s. 44). Evren için 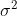, örneklem için s2, V(x), Var(x) ifadeleri kullanılır.
Varyans ölçüsünün birimi formülden ve tanımdan kolayca anlaşılacağı üzere ölçülmek istenen değişkenin ölçü biriminin karesidir. Bu durumda, verilerin açıklanmasında tercih edilmemektedir (Özdamar, 2013, s. 184). Ancak hipotez testleri gibi ileri istatistiksel yöntemlerden sıklıkla karşınıza çıkmaktadır (Alpar, 2016, s. 97). Varyans sıfır (0) ise veri setindeki yaygınlık (dağılım/ değişim) yoktur. Varyans değeri artıkça dağılımdaki değişim artmaktadır. Varyans hesaplanabilmesi için aritmetik ortalamaya ihtiyaç duyulduğundan dolayı kesikli değişkenlerde hesaplanması pek mümkün olmamaktadır (Muijs, 2004, s. 107 ).

Varyans hesaplamak neden önemlidir?
Bazen araştırmacılar verilerinin dağılımı temsil için varyans değerini kullanmak isteyebilirler. Standart sapmanın karesi olarak hesaplandığı için toplanan verilerin ölçü biriminin karesi biçimindedir ve bu durum varyans değerinin yorumlanmasını zorlaştırır. Ancak ileri istatistik tekniklerinde (Varyans Analizi ve Açımlayıcı Faktör Analizi gibi) sıklıkla kullanılan bir ölçü birimi olduğundan makalelerde raporlanması tavsiye edilir.

Örnek: Üniversite öğrencilerinin istatistik dersine karşı tutum değerlerini merak eden bir araştırmacı bir tutum ölçeği ile topladığı verileri aşağıda listelenmiştir.

Veri seti için tıklayınız.
Kodeks Editör
Xn x (puan)
X1 90
X2 88
X3 88
X4 85
X5 85
X6 85
X7 77
X8 77
X9 70
X10 70
X11 70
X12 70
X13 70
X14 68
X15 65
X16 65



SPSS hesaplaması: 

       1.      Yol
SPSS paket programındaki Analyze kısmındaki descriptive statistics sekmesindeki frequencies tıklanır. Varyansı istenen değişken sağ sütuna aktarılır ve statistics sekmesi tıklanır. Son aşamada ekrana çıkan sayfadaki dispersion kısmından variance tıklanır ve continue tuşuna basarak devam edilir. Son olarak çıkan kısımda OK butonu tıklandığında otomatik olarak analiz yapılıp output yani çıktı sayfası ekrana gelecektir.
        2.      Yol

SPSS de varyansı hesaplamanın birkaç farklı yolu vardır bunlardan bir diğer ise Analyze kısmındaki descriptive statistics sekmesi altında bulunan descriptive seçeneğidir. Bu seçenekte de araştırılmak istenen değişken sağ sütuna atılır ve options butonuna tıklanır. Açılan penceredeki dispersion bölümünde variance işaretlenir. Ardından continue tuşuna basılması gerekmektedir. Son olarak OK butonuna basıldığında varyans hesaplanır. 
Sonuçların Yorumlanması
Yukarıdaki tablolar incelendiğinde iki tabloda da aynı sonuçların olduğu gözlemlenmektedir. Tablolarda variance olarak tanımlanan değer üniversite öğrencilerinin istatistik dersine karşı tutumlarının varyansıdır ve 80,796 olarak hesaplanmıştır. Bu değer aynı zamanda standart sapmanın karesidir ( (8,989)2 = 80,796).

Sonuçların Raporlanması
Standart sapma gibi merkezi yayılım ölçüleri tek başlarına çok bilgi içermedikleri için ortalama ile beraber raporlanır. Akademik çalışmalarda en çok raporlanan ölçü birimi standart sapmadır. Ancak zaman zaman varyans değerleri de araştırmalarda yer alır.
Tablo
İstatistik Tutumlarına ait Betimsel İstatistikler
Ortalama
Varyans
İstatistiksel Tutum
76,44
80,79


Not: Yukarıdaki tablo APA 6 stiline göre hazırlanmıştır. Tablonun Word haline ulaşmak için tıklayınız.


Kaynakça
Alpar, R. (2016). Uygulamalı çok değişkenli istatistiksel yöntemler. Ankara: Detay Yayıncılık.
Muijs, D. (2004). Doing quantitative research in education with SPSS. Thousand Oaks, CA: Sage.
Özdamar, K. (2013). Paket programlar ile istatistiksel veri analizi-1: SPSS-MINITAB. Eskişehir: Nisan Kitapevi.
Turgut, M. F., & Baykul, Y. (2014). Eğitimde ölçme ve değerlendirme. Ankara: Pegem Akademi.

Bu metine atıfta bulunmak için: Karakaya Özyer, K. (2019). Varyans [Blog]. Retrieved 24 June 2022, from https://nicelanalizlericindesteksistemi.blogspot.com/.